http://cafe.naver.com/graphicsprogramming/6
http://cafe.naver.com/graphicsprogramming/6
근데 사이트가 없어짐....
0. 들어가며
Shader X2 를 살펴 보기 이전에 쉐이더가 무엇인지에 대해서 살펴 보고 가야 할 것 같습니다.
물론 책을 보는 것이 더 빠를 수도 있겠지만 저같은 허접이 한 번 정리해 보는 것도 쉽게 접근할 수 있는 방법이 되지 않을까 생각합니다.
1. Fixed Pipeline
보통 게임 프로그래밍을 한다고 하면 C/C++ 에 대해서 공부하고, Win32 나 MFC 응용프로그램을 작성하고, 그리고 나서 OpenGL 이나 Direct3D 같은 라이브러리를 응용프로그램에 통합하여 사용하게 됩니다.
Direct3D 튜토리얼이나 입문 서적들을 보면서 장치, 정점 버퍼, 인덱스 버퍼, 텍스처, 변환, 광원, 재질 등에 대해서 공부하게 됩니다. 제일 간단한 형태가 아래와 같은 구현이겠죠.
장치 생성
정점 버퍼 생성
인덱스 버퍼 생성
텍스처 생성
Clear()
BeginScene()
각종 렌더 스테이트 설정
정점 스트림 설정
인덱스 스트림 설정
광원 설정
재질 설정
텍스처 설정
각종 텍스처 스테이지 스테이트 설정
각종 샘플러 스테이트 설정
텍스처 설정
뷰행렬 설정
투영행렬 설정
월드 행렬 설정
DrawXXX()
EndScene()
Present()
텍스처 언로드
인덱스 버퍼 언로드
정점 버퍼 언로드
장치 언로드
뭐 빠진 부분도 있겠지만 BeginScene() 과 EndScene() 사이에 여러 가지 상태를 설정하고 Draw() 한 다음에 장치에 제출(Present)하게 됩니다. 이러한 일련의 과정들을 수행하기 위해서 Direct3D9 는 여러 가지 함수들을 제공합니다.
하지만 자세히 살펴 보면 이러한 여러 가지 작업들은 자료(Data) 와 연산(Operation) 으로 구분할 수 있다는 것을 알 수 있습니다.
SetXXX() 를 통해 설정하는 광원, 재질, 텍스처, 정점, 인덱스, 행렬 등은 응용프로그램에서 준비한 자료라 할 수 있고, 각종 SetXXXState() 메서드는 실제 그래픽 카드 내에서의 연산 방식을 설정하는 것이라 할 수 있습니다. 물론 이 연산에는 조건이라는 부분도 포함이 됩니다.
예를 들어 하나의 메시(Mesh) 를 렌더링한다고 합시다. 메시는 Max 등의 모델링 툴을 통해서 생성되거나 프로그래머가 직접 정점 위치를 설정하여 만들어 낼 수 있습니다. 보통 메시 자체의 공간인 오브젝트 공간을 가지고 있으며, 이를 3D 월드 내에서 표현하기 위해서는 월드 변환을 수행해 주어야 합니다. 그 다음으로는 보이지 않는 데이터들에 대한 처리 비용을 줄이기 위해서 뷰 공간으로 이동하고, 최종적으로 화면에 투영하기 위해서 절단 공간으로 이동하게 됩니다.
이러한 과정들을 처리하기 위해서 우리는 아래와 같이 간단하게 행렬들을 설정합니다.
m_pD3DDevice->SetTransform( D3DTS_WORLD, &mWorld ); // 월드 행렬
m_pD3DDevice->SetTransform( D3DTS_VIEW, &mView ); // 뷰 행렬
m_pD3DDevice->SetTransform( D3DTS_PROJECTION, &mProj); // 투영 행렬
내부적으로는 어떤 식으로 처리되든지 우리는 개념적으로 파악하고 있기만 하면 되고 모든 계산은 라이브러리 및 GPU 가 알아서 해 줍니다.
안개를 설정할 때도 마찬가지로 자료와 연산의 종류만 설정해 주면 됩니다. 안개 이론이 어쩌고 저쩌고 알지 못해도 간단하게 몇 줄 호출함으로써 이를 구현하는 것이 가능합니다.
float Start = 0.5f,
End = 0.8f;
g_pDevice->SetRenderState(D3DRS_FOGENABLE, TRUE);
g_pDevice->SetRenderState(D3DRS_FOGCOLOR, Color);
g_pDevice->SetRenderState(D3DRS_FOGVERTEXMODE, D3DFOG_LINEAR);
g_pDevice->SetRenderState(D3DRS_FOGSTART, *(DWORD *)(&Start));
g_pDevice->SetRenderState(D3DRS_FOGEND, *(DWORD *)(&End));
D3DRS_FOGENABLE 에서 안개를 렌더링하라고 조건을 설정한 것이며,
D3DRS_FOGCOLOR 는 안개 색상을 설정하고,
D3DRS_FOGVERTEXMODE 는 안개 연산을 위한 알고리즘을 설정하고,
D3DRS_FOGSTART 와 D3DRS_FOGEND 는 안개의 시작 및 종료를 설정합니다.
매우 간단하지 않습니까. 안개를 렌더링하는 알고리즘은 D3DFOG_EXP, D3DFOG_EXP2 등으로 간단히 대체될 수도 있습니다.
우리는 단순하게 FOG 를 사용할 것임을 설정하고 관련 자료 및 연산을 "미리 정해진 형식"으로 설정하기만 하면 됩니다.
이렇게 "미리" 정해진 연산을 수행할 수 있도록 제공되는 기능이 바로 고정함수 파이프라인(Fixed Pipeline)입니다.
2. Shader, Programmable Pipeline
고정함수 파이프라인을 이용해서 왠만한 것들을 표현하는 것이 가능합니다. 하지만 시간이 지날 수록 사람들은 고정함수 파이프라인이 제공하지 않는 다른 특별한 표현을 하고자 하는 욕망을 품게 되었으며, 고정 함수 파이프라인의 성능에 대한 의구심을 품게 되었습니다.
예를 들면 "D3DFOG_LINEAR, D3DFOG_EXP, D3DFOG_EXP2 가 아니라 Volume Fog 를 사용하고 싶어요" 같은 요구가 생겨나게 된 것입니다. D3D 가 고정적으로 지원하는 기능이 아니기 때문에 사용자가 직접 구현해야 할 필요가 생긴 것입니다.
이러한 요구를 받아 들여 하드웨어 제조 업체와 마이크로 소프트는 Vertex Shader 와 Pixel Shader 라는 것을 발표하게 됩니다. 이 쉐이더를 사용하는 일련의 작업들은 하드웨어 상에서 처리되는 작업들에 대한 코드를 프로그래머가 직접 조작할 수 있다는 의미에서 프로그래밍 가능한 파이프라인(programmable pipeline) 이라고 불립니다.
Vertex Shader 는 정점 처리에 대한 부분이고 Pixel 쉐이더는 픽셀 처리에 대한 부분입니다. Pixel 쉐이더는 fragment 쉐이더라고 불리기도 하는데, 개인적으로는 프래그먼트 쉐이더가 더 정확한 의미를 전달한다고 생각합니다. 일반적으로 픽셀이라는 것은 화면에 찍히는 점 하나를 의미합니다. 하지만 프래그먼트는 그 점이 계산하기 위해서 필요로 하는 여러 가지 정보들을 모두 포함하는 개념입니다.
여기에서 우리가 눈치챌 수 있는 사실은 어떤 자료를 가지고 작업을 하느냐에 따라서 XXX Shader 라는 이름이 붙는다는 것입니다. 물론 자료에 따라서 수행할 수 있는 연산들은 다르겠죠. 이 시점에서 우리는 Direct3D 아키텍처를 살펴볼 필요가 있습니다.
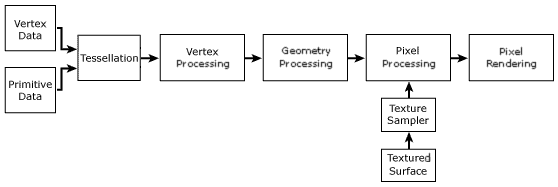
Vertex Data 와 Primitive Data 는 Tessellation 을 거쳐, Vertex processing, Geometry Processing, Pixel Processing, Pixel Rendering 의 과정을 밟습니다. 이것을 보통 그래픽 파이프라인이라고 부르는 거죠.
만약 우리가 Tessellation 에 개입할 수 있다면 ( 프로그램 코드를 작성하여 원하는 대로 할 수 있다는 의미입니다 ), Tessellation Shader 라고 부르겠죠.
Direct3D 가 Vertex Shader 와 Pixel Shader 를 제공한다는 것은 위의 그림에서 Vertex Processing 과 Pixel Processing 부분에 대한 실행 코드를 프로그래머가 작성할 수 있게 한다는 의미입니다.
현재 Direct3D 9 에서는 Vertex Shader 와 Pixel Shader 만을 지원하고 있지만 Direct3D 10 부터는 Geometry Shader 와 Rasterize Shader 를 지원한다고 합니다. 즉 하드웨어 상에서 Primitive 단위로 연산을 수행할 수 있다는 의미입니다. 아직 쉐이더에 익숙하지 않으신 분들은 그것이 어떤 의미를 가지는 지에 대해 잘 못 느끼시겠지만, 간단한 예를 들면 "마우스가 올라간 삼각형을 빨갛게 만들어 주세요" 라는 식의 작업을 Geometry Shader 에서 할 수 있다는 것입니다.
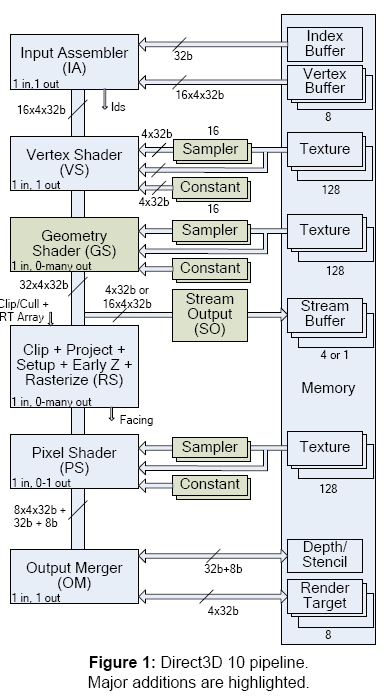
아래 그림은 Direct3D 10 의 파이프라인 개념도입니다.
그림만 보고 쉽게 이해하기는 어렵겠지만 VS, GS, RS, PS, 이렇게 네 개의 쉐이더를 지원한다는 것만 알고 계시면 될 것 같습니다. Direct3D9 의 architecture 와는 약간 다른 형태를 띠고 있기는 하지만 큰 부분에서의 차이는 없기 때문에 Direct3D9 architecture 및 쉐이더에 대해서 이해하는 것은 중요하다고 할 수 있습니다.
입니다. 또 계산기를 두들겨 보면 다음과 같이 나옵니다.
값이 0보다 크면 앞쪽에, 0보다 작으면 뒷쪽에 있는것으로 판별 합니다.